Inhalt
- Eine Normalverteilungskurve
- Normalverteilung
- Excel-Normalverteilungsfunktion (NORM.DIST-Funktion)
- Syntax für die Normalverteilungsfunktion
- Beispiel für den linken Schwanz
- Excel-Berechnung - Beispiel für den linken Schwanz
- Normalverteilung - linker Schwanzbereich
- Beispiel für den rechten Schwanz
- Excel-Berechnung - Beispiel für den rechten Schwanz
- Normalverteilung - rechter Schwanzbereich
- Beispiel für den mittleren Bereich
- Excel-Berechnung - Beispiel für den mittleren Bereich
- Normalverteilung - Mittelbereich
- Die Excel 2019 Bibel
- Verweise
Joshua ist ein Doktorand an der USF. Er interessiert sich für Business-Technologie, Analytik, Finanzen und Lean Six Sigma.
Eine Normalverteilungskurve
Normalverteilung
Die Normalverteilung ist eine sehr häufige kontinuierliche Wahrscheinlichkeitsverteilung in der Wahrscheinlichkeitstheorie. Die Normalverteilung wird oft als Glockenkurve bezeichnet, obwohl andere Verteilungen ebenfalls eine glockenförmige Kurve haben. Diese Verteilung ist nützlich, da die Eigenschaften des zentralen Grenzwertsatzes die Verwendung in vielen Anwendungen ermöglichen.
Excel-Normalverteilungsfunktion (NORM.DIST-Funktion)
Die Normalverteilungsfunktion zeigt die Normalverteilung an, wenn der Funktion ein bestimmter Mittelwert, eine Standardabweichung, ein x-Wert und eine Funktionsbestimmung hinzugefügt werden. Die Verwendung dieser Funktion findet sich hauptsächlich in Statistiken zur Bestimmung des Bereichs in einer Normalverteilung. Beim Testen von Hypothesen, das sich im inferentiellen Bereich der Statistik befindet, wird diese Funktion in großem Umfang eingesetzt. Eine Beschreibung der NORM.DIST-Syntax finden Sie in der folgenden Tabelle.
Syntax für die Normalverteilungsfunktion
| = NORM.DIST (x, Mittelwert, Standard_Dev, kumulativ) |
|---|
x = Der zu testende Wert |
Mittelwert = Das arithmetische Mittel der Verteilung |
standard_dev = Die Standardabweichung der Verteilung |
kumulativ = FALSE oder Null, ist das prob. dass x auftreten wird |
kumulativ = WAHR oder ungleich Null, ist das prob. von kleiner als oder gleich x wird auftreten |
Beispiel für den linken Schwanz
Sagen wir zum Beispiel, dass ein Unternehmen einen durchschnittlichen Verkaufswert von 2,5 Millionen Dollar hat. Nehmen wir außerdem an, dass der Umsatz normalerweise mit einer Standardabweichung von 0,5 Millionen verteilt wird und wir den Prozentsatz des Umsatzes unter 3,5 Millionen wissen möchten. Wenn wir unsere Zahlen in eine Zelle = NORM.DIST (3.5,2.5, .5, true) einfügen, erhalten wir als Ergebnis .977. True wird für den Funktionstyp ausgewählt, da die kumulative Verteilung bis zum Punkt 3.5 angezeigt werden soll. Da das Beispiel besagt, dass wir den Prozentsatz des Umsatzes unter oder unter 3,5 ermitteln möchten, wissen wir, dass wir den Prozentsatz im linken Schwanz berechnen. Wenn diese Funktion zur Berechnung des linken Endes verwendet wird, sind nach Verwendung der Funktion NORM.DIST keine weiteren Berechnungen zulässig.
Excel-Berechnung - Beispiel für den linken Schwanz
Normalverteilung - linker Schwanzbereich
Beispiel für den rechten Schwanz
Dieses Beispiel ähnelt dem Beispiel für den linken Schwanz, da dieselben Daten verwendet werden. Der durchschnittliche Verkaufswert beträgt 2,5 Millionen Dollar, der Umsatz wird normalerweise verteilt, die Standardabweichung beträgt 0,5 Millionen Dollar und der Wert von x beträgt 3,5 Millionen Dollar. Der Unterschied besteht darin, dass wir den Prozentsatz des Umsatzes über 3,5 Millionen ermitteln möchten. Um diesen Wert finden zu können, müssen wir im Wesentlichen dieselbe kumulative Verteilung wie im vorherigen Beispiel finden und von 1 subtrahieren. Die Funktion sieht also folgendermaßen aus: = 1-NORM.DIST (3.5,2.5, .5, true ). Da wir nach allem im rechten Schwanz suchen (größer als 3,5), muss nur das Komplement des linken Schwanzes berechnet werden.
Excel-Berechnung - Beispiel für den rechten Schwanz
Normalverteilung - rechter Schwanzbereich
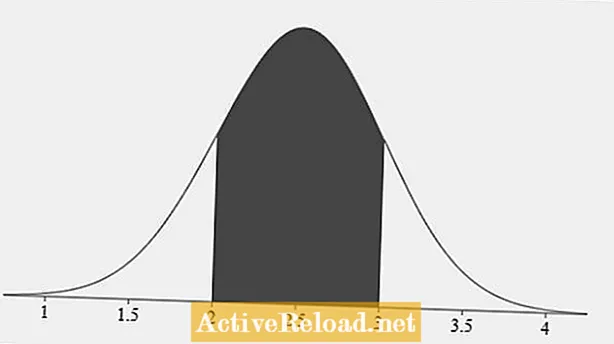
Beispiel für den mittleren Bereich
Der mittlere Bereich scheint für manche Menschen schwierig zu berechnen. Nehmen wir in diesem Beispiel an, wir verwenden immer noch 2,5 Millionen Dollar für den durchschnittlichen Umsatz, der Umsatz wird normalerweise verteilt und die Standardabweichung beträgt 0,5 Millionen Dollar. Der einzige Unterschied besteht jetzt darin, dass wir den Prozentsatz des Umsatzes zwischen 2 und 3,5 Millionen Dollar ermitteln müssen. Können Sie anhand der obigen Abbildungen der vorherigen Verteilungen herausfinden, wie Sie den mittleren Bereich finden? Sie müssen einfach die Fläche bis zu 3,5 Millionen Dollar finden und diese Fläche dann von der Fläche subtrahieren, die unter 2 angezeigt wird. Die Funktionsweise der Funktion sieht in diesem Fall folgendermaßen aus: NORM.DIST (3.5, 2.5, .5, true) -NORM.DIST (2,2,5, 0,5, wahr). Das ist wirklich selbsterklärend. Wenn Sie den gesamten Bereich links von 3,5 von dem Bereich links von 2 subtrahieren, bleibt die Mitte übrig.
Excel-Berechnung - Beispiel für den mittleren Bereich
Normalverteilung - Mittelbereich

Um mehr über das Ausführen statistischer Berechnungen in Excel zu erfahren, empfehle ich Ihnen, die Excel-Bibel zu lesen. Dies ist ein gutes Nachschlagewerk für Anfänger von Excel.
Die Excel 2019 Bibel
Verweise
- NORM.DIST-Funktion. (n.d.). Abgerufen am 15. Oktober 2018 von https://support.office.com/en-us/article/norm-dist-function-edb1cc14-a21c-4e53-839d-8082074c9f8d
- Normalverteilung. (2018, 10. Oktober). Abgerufen am 15. Oktober 2018 von https://en.wikipedia.org/wiki/Normal_distribution